nixpulvis - Euler's Identity

Euler's Identity 631 words written by Nathan Lilienthal

\[e^{\pi i} + 1 = 0\]

This equation is supremely beautiful and bewildering. It uses 5 very fundamental objects: $0$, $1$, $\pi = 3.141\ldots$, $e = 2.718\ldots$, and $i = \sqrt{-1}$, along with 4 operations: $a + b$ (addition), $a b$ (multiplication), $a^b$ (exponentiation), and finally $a = b$ (equality, identity).

\[e^{\frac{\pi i}{2}} = i \\ e^{\pi i} = (e^{\frac{\pi i}{2}})^2 = i^2 = -1 \\ e^{\frac{3\pi i}{2}} = (e^{\frac{\pi i}{2}})^3 = i^3 = -i \\ e^{2\pi i} = (e^{\frac{\pi i}{2}})^4 = i^4 = 1\]

Then it repeats…

\[e^{\frac{5\pi i}{2}} = (e^{\frac{\pi i}{2}})^5 = i^5 = i \\ \vdots\]

If you can’t see the “whole” picture yet (can anyone?), this might help. Our cyclic circular sidekicks, $\sin$ and $\cos$ are here to enlighten us.

Euler’s identity is a special case of Euler’s formula, which states:

\[e^{i \theta} = \cos(\theta) + i \sin(\theta)\]

Substitute $\pi$ (or in general, $n\pi$) for $\theta$ and we get back our identity.

\[\begin{align} \cos(\pi) + i \sin(\pi) = -1 + 0 =\ & e^{\pi i} = i^2 \\ & e^{\pi i} + 1 = 0 \end{align}\]

Tangent on Fourier Series

TODO: This information is only a sketch, and as such is somewhat sketchy.

Plot[
        sin(theta)/pi,
  (3/2) sin(theta)/pi,
  2     sin(theta)/pi,
  (5/2) sin(theta)/pi
]

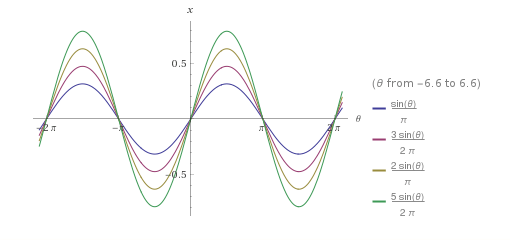
Unlike the “Euler series” we above, which is purely constructive, a square wave can be constructed with the Fourier series:

\[\sin(2 \pi \theta), \frac{1}{3} \sin(6 \pi \theta), \frac{1}{5} \sin(10 \pi \theta), ...\]

Plot[
        sin(2 pi theta),
  (1/3) sin(6 pi theta),
  (1/5) sin(10 pi theta)
]

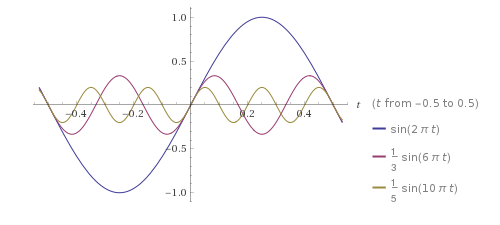
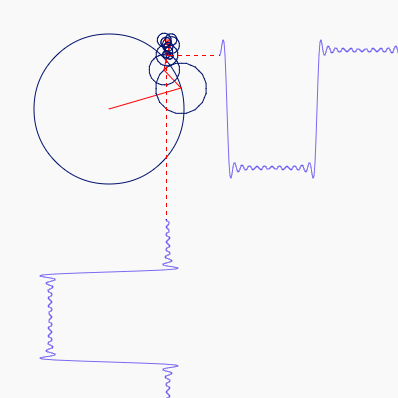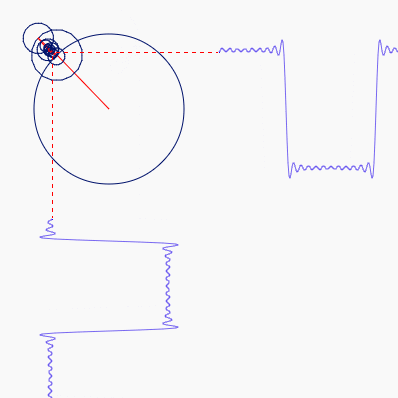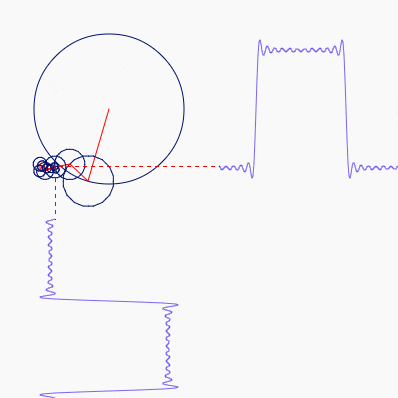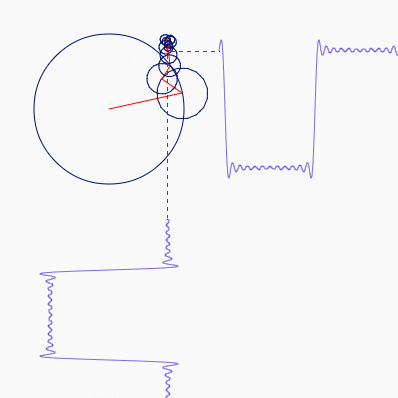
And a saw wave can be constructed by another:

\[\sin(\pi \theta), \sin(\frac{\pi \theta}{2}), \sin(\frac{\pi \theta}{4}), \ldots\]

Plot[
  sin(pi theta),
  sin((pi theta) / 2),
  sin((pi theta) / 4)
]

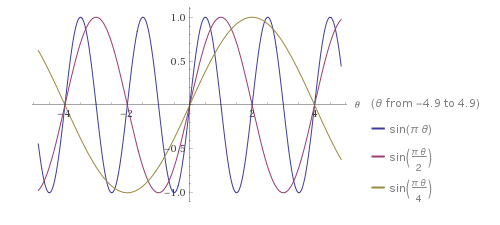
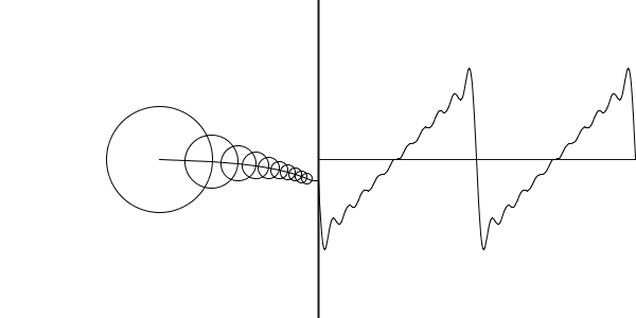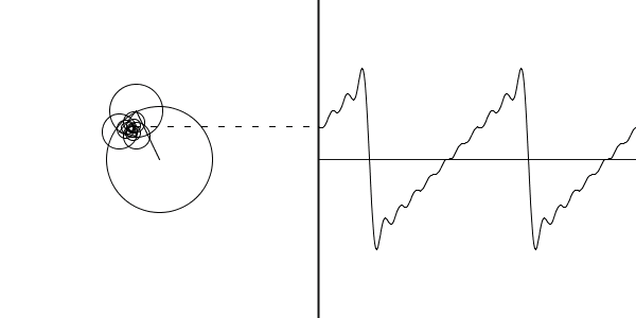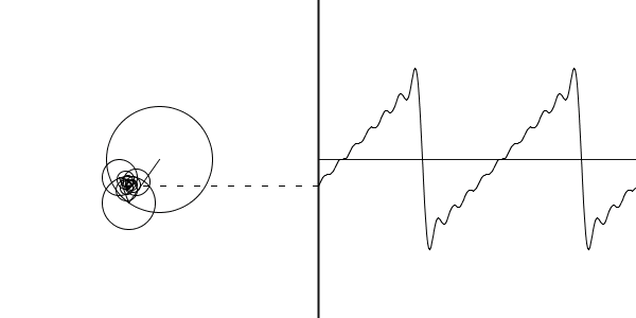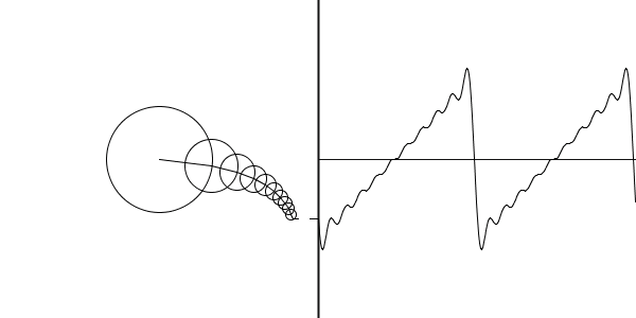
Euler’s identity can be geometrically interpreted as saying that rotating any point $\pi$ radians around an origin of a complex plane has the same effect as reflecting the point across the origin.

– Wikipedia

Fundamentally, Euler’s Identity is a root of unity, meaning that it is a solution for $z$ in the equation $z^n = 1$.

\[z = e^{2\pi i} = i^4\]

This is the definition for a more general identity which states that the $n$th roots of unity, for $n \gt 1$, add up to $0$.

\[\sum_{k=0}^{n-1} e^{2\pi i\frac{k}{n}} = 0\]

Euler’s identity is the $n = 2$ case of this equation.

\[e^0 + e^{\pi i} = e^{\pi i} + 1 = 0\]

A fun fact from a friend.

My friend Ryan showed me an interesting approximation of $e$ which uses numbers $1, 2, 3, 4, 5, 6, 7, 8, 9$ each once:

\[e \approx \left(1 + 9^{-4^{6 \times 7}}\right)^{3^{2^{85}}}\]

This may be less surprising if we recall that $e$ can be defined as:

\[e = \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n\]

So we have $n \gets 3^{2^{85}} \approx \left(9^{-4^{6 \times 7}}\right)^{-1}$, which substituting in the above, gives an approximation of $e$.

Wanna compute e in Brainfuck?

$$ \hphantom{nothing} \\ e = 2.718281828459\ldots $$


git clone https://github.com/nixpulvis/brainfuck
cd brainfuck
cargo run fixtures/e.bf


>>>>++>+>++>+>>++<+[
  [>[>>[>>>>]<<<<[[>>>>+<<<<-]<<<<]>>>>>>]+<]>-
  >>--[+[+++<<<<--]++>>>>--]+[>>>>]<<<<[<<+<+<]<<[
    >>>>>>[[<<<<+>>>>-]>>>>]<<<<<<<<[<<<<]
    >>-[<<+>>-]+<<[->>>>[-[+>>>>-]-<<-[>>>>-]++>>+[-<<<<+]+>>>>]<<<<[<<<<]]
    >[-[<+>-]]+<[->>>>[-[+>>>>-]-<<<-[>>>>-]++>>>+[-<<<<+]+>>>>]<<<<[<<<<]]<<
  ]>>>+[>>>>]-[+<<<<--]++[<<<<]>>>+[
    >-[
      >>[--[++>>+>>--]-<[-[-[+++<<<<-]+>>>>-]]++>+[-<<<<+]++>>+>>]
      <<[>[<-<<<]+<]>->>>
    ]+>[>>>>]-[+<<<<--]++<[
      [>>>>]<<<<[
        -[->--[<->+]++<[[>-<+]++[<<<<]+>>+>>-]++<<<<-]
        >-[+[<+[<<<<]>]<+>]+<[->->>>[-]]+<<<<
      ]
    ]>[<<<<]>[
      -[
        -[
          +++++[>++++++++<-]>-.>>>-[<<<----.<]<[<<]>>[-]>->>+[
            [>>>>]+[-[->>>>+>>>>>>>>-[-[+++<<<<[-]]+>>>>-]++[<<<<]]+<<<<]>>>
          ]+<+<<
        ]>[
          -[
            ->[--[++>>>>--]->[-[-[+++<<<<-]+>>>>-]]++<+[-<<<<+]++>>>>]
            <<<<[>[<<<<]+<]>->>
          ]<
        ]>>>>[--[++>>>>--]-<--[+++>>>>--]+>+[-<<<<+]++>>>>]<<<<<[<<<<]<
      ]>[>+<<++<]<
    ]>[+>[--[++>>>>--]->--[+++>>>>--]+<+[-<<<<+]++>>>>]<<<[<<<<]]>>
  ]>
]

This program computes the transcendental number e, in decimal. Because this is
infinitely long, this program doesn't terminate on its own; you will have to
kill it. The fact that it doesn't output any linefeeds may also give certain
implementations trouble, including some of mine.

(c) 2016 Daniel B. Cristofani
http://brainfuck.org/