Graph Notation 544 words published on August 15, 2025.

Expressing graphs is a useful thing to be able to do. Most libraries I’ve seen in the past give you a way to declare nodes and edges directly. In some applications this is the most natural way to express the graph, when edges are somewhat ad-hoc.

However, when working on a design for Secure Multiparty Computations we often needed a way to express graphs with more global notions of fully-connectedness. This got me thinking… could we use that as a primitive to build arbitrary graphs? The answer appears to be yes!

Fully Connected Graphs

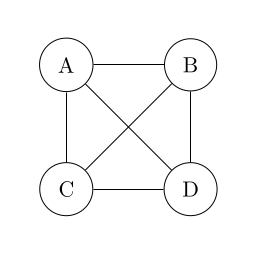
Sets of fully connected nodes are denoted with {}, for example the following shows a simple fully-connected graph of four nodes.

G = {A, B, C, D}

We can nest expressions within each other:

G = { {A, B}, {C, D} }

The two examples above are equivalent, however it may be useful to label specific groups of nodes anyway.

X = {A, B}
Y = {C, D}
G = {X, Y} = {A, B, C, D}

Fully Disconnected Graphs

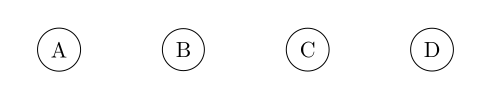
We can also define fully disconnected graphs with [].

G = [A, B, C, D]
  = [[A, B], [C, D]]

Star Graphs

While a disconnected graph may seem useless by itself, when nested within a larger connected graph they allow us to represent arbitrarily complex topologies of graphs (we should prove this true!). To accomplish this, we say that connectedness distributes:

{A, [B,C]} = [{A, B}, {A, C}]

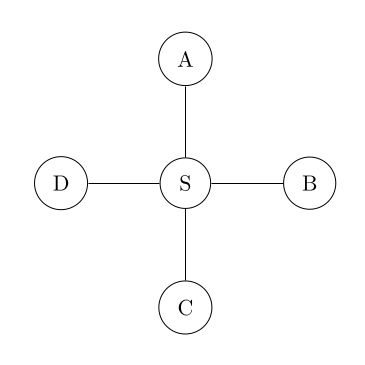
For example a “star” graph with four edge nodes and a single center node can be represented like this:

G = { S, [A, B, C, D] }
  = [{S, A}, {S, B}, {S, C}, {S, D}]

Example Reduction

Here we show that starting with a graph description G, we end up with an equivalent graph description G' through a series of reductions.

We define G to be a graph of a disconnected [A,B], connected to C, all disconnected from D, finally connected to E. We can interpret this more naturally by thinking of the fully connected graph {A,B,C,D,E}, then removing connections to maintain the property that [A,B] and [D, {A,B,C}] are disconnected.

G  = {[{[A,B],C},D],E}
   -distributeC>
     {[[{A,C},{B,C}],D],E}
   -flatten>
     {[{A,C},{B,C},D],E}
   -distributeE>
G' = [{A,C,E},{B,C,E},{D,E}]

As you can see in the final, normal form, A and B are never connected, and neither is D connected with any node other than E, which is precisely what we asked for.

---

This was originally a thought experiment in Achilles’ Tent Note #12, but I think it’s a fun way to express arbitrary graphs. I’m not sure how novel (or complete) it is however, but I thought I’d unbury it a bit in case someone else finds it interesting. I’ve also trimmed the contents of the original post a bit to remove the stuff related to MPC, which is completely outside the scope of this post, and expanded on a few things.